😮 Самое большое число | Интересные факты
Каждого рано или поздно мучает вопрос, а какое же самое большое число. На вопрос ребенка можно ответить миллион.
А что дальше? Триллион. А еще дальше? На самом деле, ответ на вопрос какие же самые большие числа прост. К самому большому числу просто стоит добавить единицу, как оно уже не будет самым большим. Процедуру эту можно продолжать до бесконечности.
А если же задаться вопросом: какое самое большое число существует, и какое у него собственное название? Вот на этот вопрос можно ответить. На самом деле сейчас есть две системы наименования чисел – английская и американская.
Число Пи — одно из самых таинственных
Американская – довольно простая. Названия больших чисел строятся следующим образом: сначала идет латинское порядковое числительное, а затем добавляется суффикс «иллион». Исключение – миллион, что значит тысяча. Далее получаются числа: триллион, квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион и дециллион.
Такую систему используют в США, Канаде, России и Франции.
Английская система более распространенная в мире. Ее используют в Испании и Великобритании, а так же в ряде других стран. Здесь названия стоятся так: к латинскому числительному прибавляют суффикс «иллион», к следующему числу (которое больше в 1000 раз) уже добавляют суффикс «иллиард». То есть после триллиона идет триллиард, после квадриллион, квадриллиард и так далее. Получается, что по английской и американской системам одни и те же большие числа называются по-разному.
В русский язык из английской системы пришел только миллиард (10 9), который американцы называют биллионом. Иногда в России употребляют слово триллиард, то есть 1000 триллионов или квадриллион.
Нас окружают миллионы чисел
Кроме чисел, которые записаны при помощи английской или американской систем, известны так называемые внесистемные числа. То есть те, у которых есть свои собственные названия, в них нет латинских префиксов. Их несколько, вернемся к ним чуть позже.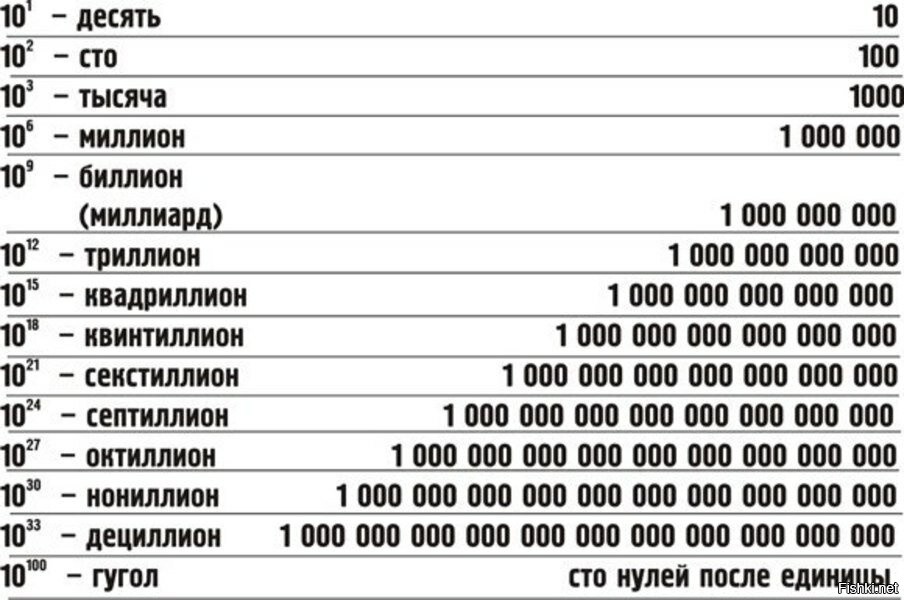
А пока рассмотрим запись латинскими числительными. Оказывается, ими можно записывать числа не до бесконечности. Единица – это 10 0 , десять — 10 1, и так далее, миллиард — 10 9, триллион — 10 12, квадриллион — 10 15, квинтиллион — 10 18, секстиллион — 10 21, септиллион — 10 24, октиллион — 10 27, нониллион — 10 30, дециллион — 10 33. А что же дальше? На самом деле можно с помощью приставок и дальше рождать числа-монстры: андециллион, дуодециллион, тредециллион и так далее. Но нам нужны собственные названия чисел, а тут только составные названия. Поэтому по этой системе собственных имен может быть еще только три вигинтиллион — 10 63, центиллион — 10 303, миллеиллион — 10 3003.
Число гугол
Поэтому, по этой системе числа с собственным, а не составным названием больше 10 3003 получить невозможно. Однако числа больше миллеиллиона есть и известны – это внесистемные числа.
Самое маленькое такое число носит название мириада. Оно даже есть в словаре Даля. Означает оно сотню сотен, то есть 10 тысяч. Слово, правда, не используется по назначению. Оно употребляется как не определенное число, а бесчисленное множество чего-либо.
Далее идет гугол. Это десять в сотой степени. Единица со ста нулями. О гуголе впервые написали в 1938 году. Американский математик Эдвард Каснер сказал, что назвать большое число таким образом предложил его племянник. А популярным это название стало после того, как в честь него назвали поисковую систему «Google». Далее встречается число асанкхейя. Это 10 140. Общепринято, что этому числу равно количество космических циклов, которые необходимы для обретения нирваны. Следом идет число гуголплекс. Его придумал тот же Каснер с племянником. Оно означает 10 10100. Или единица с гуголом нулей.
Вспомним математику
Еще больше гуглоплекса число Скьюза. Его предложил Скьюз в 1933 году во время доказательства гипотезы Риманна о простых числах.
Оно означает eee79. То есть e в степени e в степени e в степени 79. Позже Риел свел число Скьюза к ee27/4. Это приблизительно равно 8,185•10 370. Раз это число зависит от e, значит оно не целое. Следовательно, рассматривать его не будем.
Есть второе число Скьюза. Обозначается оно как Sk2. Оно вводится, если гипотеза Риманна не справедлива. Второе число Скьюза равно 1010101000. Чем больше в числе степеней, следователь тем сложнее понять, какое же из чисел больше. Поэтому для сверхбольших чисел пользоваться степенями неудобно. Уже придуманы числа, у которых степени степеней не вылезают за страницу. Математики придумали несколько принципов для их записи. Правда, у каждого ученого был свой принцип записи, некоторые не связаны друг с другом. Хьюго Стейнхауза предложил записывать очень большие числа внутри геометрических фигур. К примеру, — это nn. — это «n в n треугольниках». — это «n в n квадратах». Все тот же Стейнхауз придумал два новых больших числа. — мега, а число — мегистон.
Число Фибоначчи
Эта нотация была доработана математиком Лео Мозером.
По ней можно записать числа, которые больше мегистона. Здесь не надо рисовать круги в кругах. А достаточно после квадратов рисовать не круги, а пятиугольники, затем шестиугольники. Таким образом, Мозер записал стейнхаузовскую мегу 2[5], а мегистон 10[5]. Он же предложил называть многоугольник с количеством сторон равным меге – как мегагон. А число 2 в Мегагоне2[2[5]]. Это число получило название число Мозера.
Но и это число не самое большое. Самое большое число, которое применяется в математическом доказательстве, это Число Грэма. Его использовали впервые в 1977 году в доказательстве оценки в теории Рамсея.
Оригинальный способ умножения больших чисел
Оно выражено в особой 64-уровневой системе, поскольку связано с бихроматическими гиперкубами. Вывел систему Кнут в 1978 году. Он придумал понятие сверхстепень и предложил записывать ее стрелками вверх. В итоге, число Грэма G63 или просто G и является самым большим числом в мире. Оно даже попало в Книгу рекордов Гиннеса. Последние 50 цифр числа Грэма — это ./BiggerThanMillion-58b734085f9b5880803990ff.jpg)
..03222348723967018485186439059104575627262464195387.
Самое большое число в мире — это число Грэма
Миллион, миллиард (или биллион?), триллион… С каждым разом представлять такие числа все труднее. Чего уж говорить про гугол (единица с сотней нулей) и невообразимый гуголплекс.
Чтобы полностью изобразить гуголплекс, не хватит ни одного листка бумаги. Более того, даже самой Вселенной. Возьмем самую маленькую ручку, что сможем придумать, и будем рисовать на каждом атоме, и все равно из этого ничего не выйдет. Фантастика в фантастике, не иначе!
А почему бы не пойти дальше и не возвести гуголплекс в степень гуголплекс? Звучит абсурдно и бессмысленно. Однако есть число, которое является не только единицей с большим количеством нулей. У него также есть практическая сторона. Встречайте: число Грэма!
Число названо в честь математика Рональда Грэма. Впервые оно появилось в работе, посвященной решению одной из задач в теории Рамсея, другого математика.
Её условия были достаточно абстрактны, понятны и слегка безумны. Рассчитана задача на знание комбинаторики.
Представьте себе куб, все вершины которого соединены линиями–отрезками двух цветов, красного или синего. Соединены и раскрашены в случайном порядке. Необходимо было подобрать такой комбинацию синих и красных ребер фигуры, чтобы при этом не было четырех вершин одного цвета в одной плоскости.
Задача вполне себе разрешима, но из-за простоты ученые её стали усложнять. Любят же они себя испытывать!
Сначала из куба сделали тессеракт — куб с четырьмя измерениями! Но даже так решение быстро нашли. Затем попробовали с пятью, шестью а затем с семью измерениями…. Тут-то и возникла проблема при подсчетах.
Грэм не сумел математически доказать возможность выполнения условий задачи в семимерном, восьмимерном, девятимерном кубе. Однако было недостаточно сказать «я не могу!», чтобы потом всему миру заявить: «это невозможно!». Нужно еще это математически как-то доказать.
3 (три в степени три, что тоже в степени три).
Стрелочка показывает наличие пирамиды из степеней.
Чтобы вы понимали:
3↑↑3 = 7 625 597 484 987
3↑↑↑3 = башня, высотой от Земли до Марса.
3↑↑↑↑3 = число, которое невозможно ни представить, ни описать.
Число g₁ и есть 3↑↑↑↑3. g₂ — это те же тройки, только количество стрелочек между ними равняется количеству числа g₁.
И так каждый раз, пока не дойдем до числа Грэма: G=g64.
По-другому записать его не удастся. Как уже было сказано, банально места не хватит.
Математика способна удивлять. Будучи на грани фантастики, она двигает науку вперед, сама создает крышесносные теории и сама же их подтверждает. Ну, как сама. Этим занимаются неординарные персоны, чья сохранившаяся детская наивность позволяет идти на удивительные свершения в области науки. Математика — это не только гигантские числа; это также люди, которые трудятся и изобретают на благо всему обществу.
Полюбить науку с детства очень важно.
Математику — еще важнее. Изучая её, изучаешь историю, культуру, физику и другие отрасли научного знания.
В Матклассе продолжают работать онлайн-кружки и курсы по математике для детей от 5 до 99 лет. Также, если ситуация стабилизируется, скоро заработают и занятия в Москве и Калининграде!
Детям нравится изобретать, они получают настоящее удовольствие, когда их логические способности и фантазия оказываются полезными на практике. Так давайте подарим им такой опыт!
Узнайте, как мы учим детей думать на наших онлайн-кружках математики
Какое самое большое число в мире?
Мы не можем прямо ответить на этот вопрос, какое самое большое число в мире, так как существует бесконечное число чисел, и самое большое число никогда не может быть записано, потому что мы всегда можем добавить 1 к любому большому числу. Поэтому числа стремятся к бесконечности. А бесконечность — это не число, а понятие.
Какое самое большое число в мире?
A Googolplex считается самым большим числом в мире.
Пишется как 10 гугол . Число 10 гугол также можно выразить в экспоненциальном формате, который будет равен . При записи числа гугол в обычном формате записи числа вероятность потери счета очень высока. Следовательно, его удобнее выразить в виде показателя степени и степени.
Число гуголплекс настолько нелепо велико, что его невозможно записать в формате записи чисел. Следовательно, число остается концепцией, поскольку оно бесполезно в математике для основных вычислений.
Итак, теперь можно спросить, а как насчет Googolpex Plus One и т. д., они больше, чем Googolpex, это правильно, но мы определяем большое число с каким-то определенным свойством, и добавление единицы к любому большому числу недопустимо.
А как же Бесконечность? Теперь бесконечность — это не число, а скорее понятие. Кто-то может возразить, что нельзя определить больше чисел, чем Googolplex. Ответ на этот вопрос — да, мы можем, и число Грэма — одно из таких чисел.
Это экспоненциально больше, чем Googolpex.
Насколько велико число Грэма?
Число Грэма смехотворно велико, оно настолько велико, что мы даже не можем представить себе это число, и этого числа в наблюдаемом числе во Вселенной недостаточно, чтобы даже написать это число.
Названо в честь известного математика Рональда Грэма, давшего понятие этого числа. Число Грэма настолько велико, что мы не можем записать его в стандартных обозначениях, но его можно выразить с помощью математических символов и обозначений.
Подробнее,
- Целые числа
- Вещественные числа
- Иррациональные числа
Часто задаваемые вопросы
900 46 Q1: Какое число в мире занесено в Книгу рекордов Гиннесса?
Ответ:
Число Грэма занесено в Книгу рекордов Гиннеса как самое большое конкретное целое число, использованное в опубликованном математическом доказательстве.
Q2: Кто пытался записать номер Googolplex?
Ответ:
Математик Вольфганг Х. Ницше попытался записать число гуголплекс и начал выпускать книги с ним.
Q3: Что такое Секстиллион?
Ответ:
Секстиллион — это число, считающее один миллион миллионов миллионов миллионов миллионов миллионов, в экспоненциальной форме оно записывается как 10 36 для длинного счета. Число символически представлено SX.
Q4: Сколько миллиардов равно одному квадриллиону?
Ответ:
1000000 миллиардов равно одному квадриллиону.
Q5: Когда-нибудь заканчиваются счетные числа?
Ответ:
Нет, числа во Вселенной бесконечны.
Вопрос 6.
Является ли бесконечность действительным числом?
Ответ:
Бесконечность не является числом, поскольку математически она не представлена в цифрах. Бесконечность — это скорее понятие, чем определенное реальное число.
Какое самое большое число? — ПОПУЛЯРНАЯ МИНУТА
http://nonfictionminute.org/nonfictionminute 13.03.2023 203 комментария
Дэвид М. Шварц Можете ли вы выразить словами, что говорят вам эти уравнения? Задумайте большое число. Как насчет одного миллиона? Это тысяча тысяч. Это много. Если вы считаете без остановки до миллиона, это займет у вас около 23 дней. Конечно, триллион — не самое большое число. Есть квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион, дециллион и другие. Каждый в тысячу раз больше предыдущего. Есть даже огромное число под названием вигинтиллион, состоящее из 63 нулей. Но вигинтиллион — креветка по сравнению с гуголом. Гугол? Обратите внимание, как это пишется: G-O-O-G-O-L, а не G-O-O-G-L-E. Гугол — это единица с сотней нулей. Он получил свое название от девятилетнего мальчика. Гугол — это больше, чем все волосы в мире. Это больше, чем все травинки и все песчинки. Это даже больше, чем количество атомов во Вселенной. Астрофизики оценивают число атомов как единицу с 82 нулями. Вам нужно добавить еще 18 нулей, чтобы получить гугол. Кстати, несколько лет назад два человека, которые изобрели новый мощный интернет-поисковик, решили назвать свой веб-сайт и компанию гигантским числом гугол. Гугол настолько велик, что практически бесполезен, но мальчик, который дал ему имя, придумал имя для еще большего числа — «гуголплекс». Гуголплекс — это единица с нулями гугола. Во всех ручках мира недостаточно чернил, чтобы написать столько нулей, но не стесняйтесь попробовать. Так значит, гуголплекс — самое большое число? А как насчет гуголплекса и одного? Два гуголплекса? Гуголплекс гуголплекс? Любое число, которое вы говорите, я могу сказать на одно больше. Я слышу, как вы спрашиваете: «А как насчет бесконечности? Разве это не самое большое число?» Извините, но бесконечность не число. Число определяет количество, а бесконечность не является количеством. Это означает «продолжаться и продолжаться вечно». И это то, что делают числа. Они продолжаются и продолжаются вечно. Бесконечность — это не число, но числа бесконечны. Думаете, вы слишком стары для азбуки? Вы подумаете еще раз, если прочитаете отрывок из книги Дэвида М. Дэвид Шварц является участником группы авторов по вызову iNK и доступен для классных программ с помощью FieldTripZoom , потрясающей технологии, для которой требуются только компьютер, Wi-Fi и веб-камера. Нажмите здесь , чтобы узнать больше MLA 8 Citation 203 комментария | Новостная лента *НОВОСТИ * Дайан Равич, премьер-министр и неутомимый чемпион государственной школы, дала большой отзыв о нас в своем блоге! НОВИНКА! *NEWSFLASH * Категории Все Категории Архив Март 2021 МИНУТА НЕФИКСАЦИИ, Авторы по вызову, и. iNK Books & Media Store являются подразделениями iNK THINK TANK INC. Для получения дополнительной информации или поддержки обращайтесь по адресу [email protected] Для получения информации о политике конфиденциальности перейдите по адресу © COPYRIGHT the Nonfiction Minute 2020. Этот сайт использует файлы cookie, чтобы персонализировать ваш опыт, анализировать использование сайта и предлагать индивидуальные рекламные акции. www.youronlinechoices.eu Архивы март 2023 г. |
Хотите считать так высоко? Вы будете в этом 95 лет. Но триллион заставляет миллиард казаться ничтожным. Триллион — это тысяча миллиардов (или миллион миллионов). На такой подсчет у вас уйдет 200 000 лет. Веселиться!
Но написали неправильно. Вот почему компания Google пишется с L-E. Но число гугол по-прежнему пишется с О-Л.
Шварца: B для двоичных чисел, F для Фибоначчи, P для вероятности… Вы можете видеть, что это книга ABC, не похожая ни на одну другую. Нажмите сюда, для получения дополнительной информации.
Мы публикуем информацию о предстоящей неделе по субботам и обновляем ее в течение недели примерно в 16:00 по восточному времени, поэтому публикация на следующий день оказывается в начале очереди. 
Наслаждаться! 
теракты
Leave a Reply