Наибольшую площадь территории имеет: Контрольный тест по Географии «Страны на современной политической карте мира»

Контрольный тест по Географии «Страны на современной политической карте мира»

Тема: Страны на современной политической карте мира

ВАРИАНТ 1

1. Государство, занимающее первое место в мире по размерам территории:

1. Австралия. 2. Канада. 3. Россия. 4. Китай.

2. Наибольшую площадь территории имеет:

1. Андорра. 2. Мальта. 3. Ватикан. 4. Польша.

3. Страна с численностью населения свыше 1 млрд. человек:

1. США. 2. Индонезия. 3. Индия. 4. Египет.

4. Государство, территория которого омывается водами трех океанов:

1. Норвегия. 2. Австралия. 3. Словакия. 4. Россия.

5. Государства, не имеющие выхода к морскому побережью:

1. Казахстан, Узбекистан, Киргизия.

2. Пакистан, Бангладеш, Таиланд.

3. ЮАР, Ангола, Сомали.

6. Республиканскую форму правления имеет:

1. Испания. 2. Бельгия. 3. Япония. 4. Бразилия.

7. К конституционным монархиям относится:

1. Бруней. 2. Катар. 3. Швеция. 4. Кувейт.

8. К парламентским республикам относится:

1. США. 2. Швейцария. 3. Египет. 4. Мексика.

9. Страна с федеративным типом государственного устройства:

1. Франция. 2. Китай. 3. Германия. 4. Испания.

10. Государства, состоящие из административно-территориальных единиц, которые напрямую подчиняются центральным органам власти и не пользуются самоуправлением, называются:

1. Теократические государства.

2. Федеративные государства.

3. Конституционные монархии.

4. Унитарные государства.

Тема: Страны на современной политической карте мира

ВАРИАНТ 2

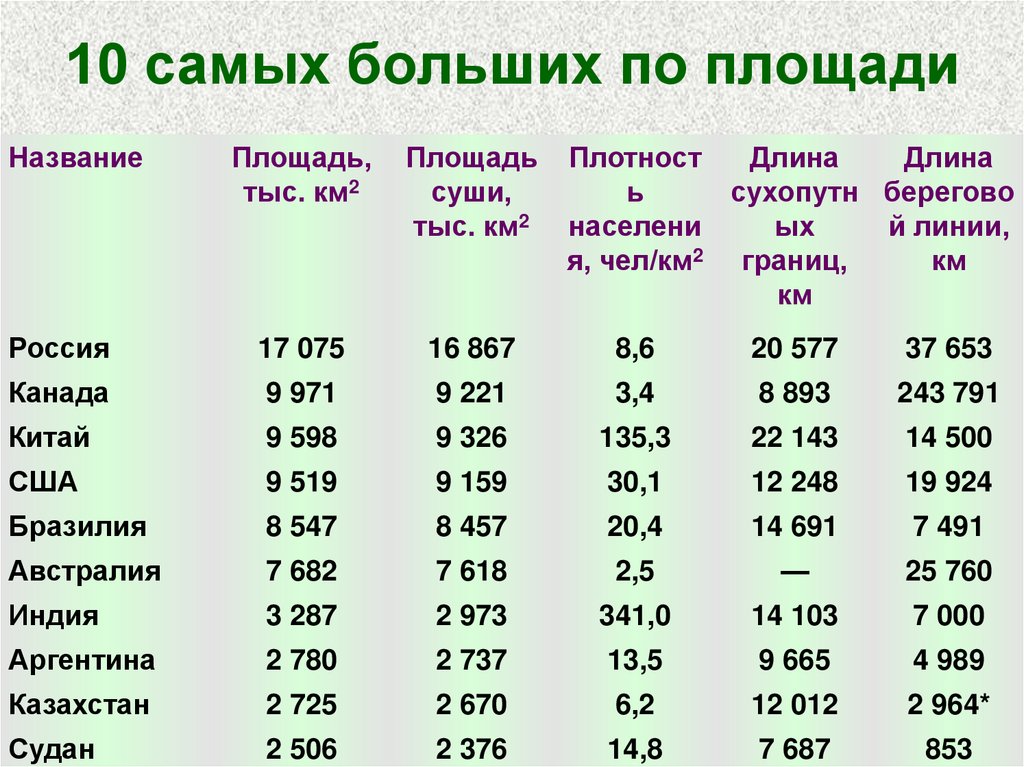
1. Крупнейшее государство по площади территории в Америке:

1. США. 2. Канада. 3. Бразилия. 4. Гватемала.

2. Наименьшую площадь территории имеет:

1. ФРГ. 2. Франция. 3. Испания. 4. Монако.

3. Страна с численностью населения свыше 1 млрд. человек:

1. Россия. 2. Япония. 3. Китай. 4. Канада.

4. Государство Латинской Америки, омываемое водами Тихого океана:

1. Бразилия. 2. Канада. 3. Куба. 4. Чили.

5. Европейское государство, не имеющее выхода к морскому побережью:

1. Литва. 2. Португалия. 3. Венгрия. 4. Испания.

6. Монархическую форму правления имеет:

1. Индия. 2. Таиланд. 3. Ирак. 4. Израиль.

7. К абсолютным монархиям относится:

1. Великобритания. 2. Нидерланды. 3. Норвегия. 4. Саудовская Аравия.

8. К президентским республикам относится:

1.Россия. 2. Италия. 3. Германия. 4. Индия.

9. Страна с унитарным типом государственного устройства:

1. Бельгия. 2. Россия. 3. Канада. 4. Монголия.

10. Государства, состоящие из политических территориальных единиц, которые, как правило, обладают значительным внутренним самоуправлением, называются:

1. Демократические государства.

2. Федеративные государства.

3. Президентские республики.

4. Конституционные монархии.

ОТВЕТЫ

Тест по учебной дисциплине География

Тема: Страны на современной политической карте мира

ВАРИАНТ 1

1.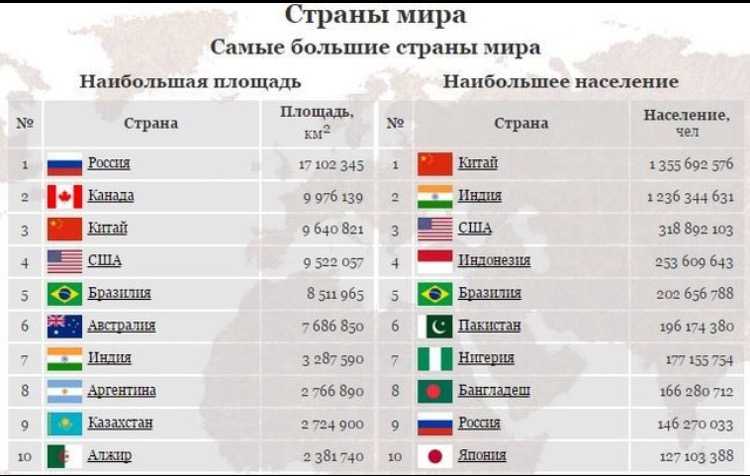 Государство, занимающее первое место в мире по размерам территории:

1. Австралия. 2. Канада. 3. Россия. 4. Китай.

2. Наибольшую площадь территории имеет:

1. Андорра. 2. Мальта. 3. Ватикан. 4. Польша.

3. Страна с численностью населения свыше 1 млрд. человек:

1. США. 2. Индонезия. 3. Индия. 4. Египет.

4. Государство, территория которого омывается водами трех океанов:

1. Норвегия. 2. Австралия. 3. Словакия. 4. Россия.

5. Государства, не имеющие выхода к морскому побережью:

1. Казахстан, Узбекистан, Киргизия.

2. Пакистан, Бангладеш, Таиланд.

3. ЮАР, Ангола, Сомали.

6. Республиканскую форму правления имеет:

1. Испания. 2. Бельгия. 3. Япония. 4. Бразилия.

7. К конституционным монархиям относится:

1. Бруней. 2. Катар. 3. Швеция. 4. Кувейт.

8. К парламентским республикам относится:

1. США. 2. Швейцария. 3. Египет. 4. Мексика.

9. Страна с федеративным типом государственного устройства:

1. Франция. 2. Китай. 3. Германия. 4. Испания.

10. Государства, состоящие из административно-территориальных единиц, которые напрямую подчиняются центральным органам власти и не пользуются самоуправлением, называются:

1. Теократические государства.

2. Федеративные государства.

3. Конституционные монархии.

4. Унитарные государства.

Тема: Страны на современной политической карте мира

ВАРИАНТ 2

1. Крупнейшее государство по площади территории в Америке:

1. США. 2. Канада. 3. Бразилия. 4. Гватемала.

2. Наименьшую площадь территории имеет:

1. ФРГ. 2. Франция. 3. Испания. 4. Монако.

3. Страна с численностью населения свыше 1 млрд. человек:

1. Россия. 2. Япония. 3. Китай. 4. Канада.

4. Государство Латинской Америки, омываемое водами Тихого океана:

1. Бразилия. 2. Канада. 3. Куба. 4. Чили.

5. Европейское государство, не имеющее выхода к морскому побережью:

1. Литва. 2. Португалия. 3. Венгрия. 4. Испания.

6. Монархическую форму правления имеет:

1. Индия. 2. Таиланд. 3. Ирак. 4. Израиль.

7. К абсолютным монархиям относится:

1. Великобритания. 2. Нидерланды. 3. Норвегия. 4. Саудовская Аравия.

8. К президентским республикам относится:

1.Россия. 2. Италия. 3. Германия. 4. Индия.

9. Страна с унитарным типом государственного устройства:

1. Бельгия. 2. Россия. 3. Канада. 4. Монголия.

10. Государства, состоящие из политических территориальных единиц, которые, как правило, обладают значительным внутренним самоуправлением, называются:

1. Демократические государства.

2. Федеративные государства.

3. Президентские республики.

4. Конституционные монархии.

ОТВЕТЫ

2 \ .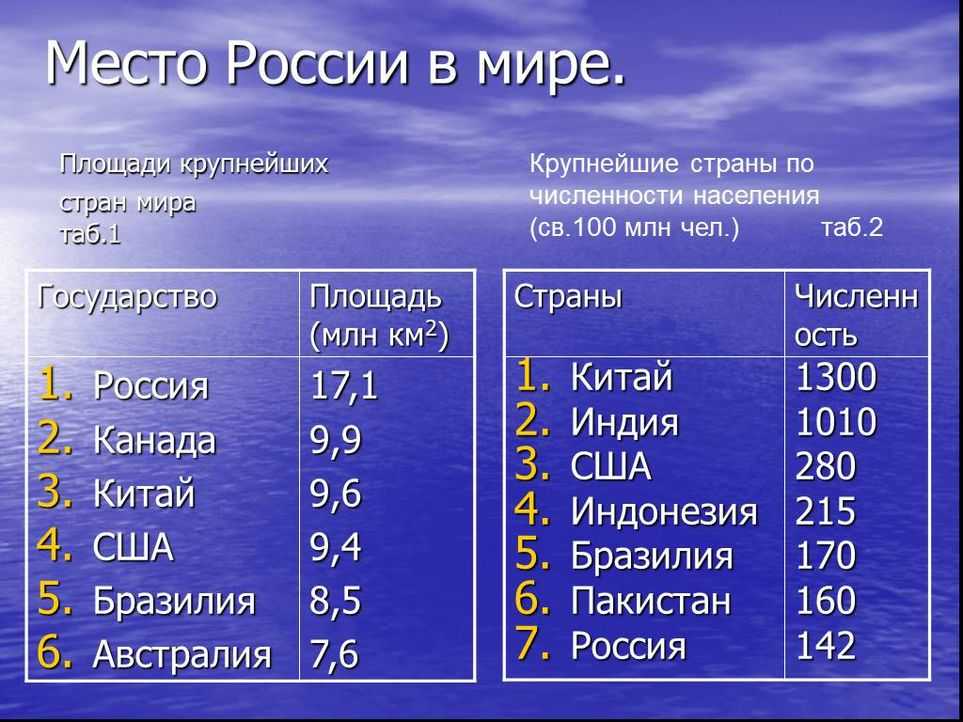
$$

То есть площадь $A$, ограниченная кривой $C$, меньше площади, ограниченной окружностью той же длины.

Что касается доказательства изопериметрического неравенства , то вот то, что я выучил на бакалавриате, оно элементарно и красиво, как мне кажется.

Обойдите кривую $C$ против часовой стрелки. Для плоского векторного поля $(P,Q)$ теорема Грина говорит:

$$
\oint_{\partial D}(Pdx + Qdy) = \int_D \left( \frac{\partial Q}{\partial x} — \frac{\partial P}{\partial y}\right) dxdy\ .
$$ 9L x’yds \ .
$$

Пока достаточно нашей кривой $C$. Давайте искать хорошую окружность для сравнения!

Прежде всего, поскольку $[0,L]$ компактна, функция $x: [0,L] \longrightarrow \mathbb{R}$ будет иметь глобальный максимум и глобальный минимум. При необходимости изменив начало нашей параметризации, я могу считать, что минимум достигается при $s=0$. Пусть максимум достигается при $s=s_0 \in [0,L]$. Пусть $q = \gamma (0)$ и $p = \gamma (s_0)$. (Если существует более одного минимума и более одного максимума, мы выбираем по одному из них: те, которые вы предпочитаете.)

Поскольку $x'(0) = x'(s_0) = 0$, у нас есть вертикальные касательные в обеих точках $p,q$ нашей кривой $C$. Нарисуйте окружность между этими параллельными линиями, касательной к ним обеим (немного дальше от $C$, чтобы не запутаться). Таким образом, радиус этой окружности будет равен $r = \frac{\| pq \|}{2}$.

Возьмем начало координат в центре этой окружности. Параметризируем его тем же $s$, длина дуги $C$:

$$
\sigma (s) = (\overline{x}(s), \overline{y}(s)) \ , \quad s \in [0, L] \ .
$$ 92 \ .
$$

геометрия — Форма наибольшей площади с диаметром 1?

Задавать вопрос

спросил
7 лет, 1 месяц назад

Изменено
1 год, 8 месяцев назад

Просмотрено
2к раз

$\begingroup$

Определите диаметр фигуры как наибольшее расстояние между любыми двумя ее точками. Какая фигура диаметром 1 имеет наибольшую площадь?

Это круг?

Какое-то время я искал самый большой маленький многогранник и снова посмотрел на самый большой маленький многоугольник. В статье Хенриона и Мессина результаты были распространены на 16-угольник. Тенденция показывает, что наилучшая область является хаотичной, при этом оптимальный 14-угольник имеет лучшее улучшение по сравнению с обычным 14-угольником на коэффициент выше, чем показано для 8-, 10- и 12-угольников.

Если тренд сохранится, может возникнуть единичный тракл, который создаст от 50 до 90 гонов диаметра 1 с общей площадью больше, чем круг диаметром 1.

Возможно, быстрее, чем это, с помощью методов полигонов Рело.

Какая форма диаметром 1 имеет наибольшую площадь? Многоугольники диаметром 1, которые не помещаются в круг диаметром 1, легко найти, но есть ли полигоны с внешней площадью, превышающей непокрытую площадь?

• геометрия
• оптимизация
• площадь
• экстремальная комбинаторика

$\endgroup$

$\begingroup$

Я думаю, что это круг по следующим рассуждениям. Я не совсем уверен в этом, поэтому, если есть ошибка, надеюсь, кто-то меня поправит.

Форма максимальной площади должна быть ограничена кривой постоянной ширины (диаметром является ширина), так как любую кривую переменной ширины можно расширить в направлениях, где ширина недостаточна, увеличивая площадь при сохранении диаметра одинаковый.

Теперь по теореме Барбье периметр любой кривой постоянной ширины $w$ равен $\pi w$, независимо от формы. Таким образом, все фигуры, которые могут быть кандидатами на оптимальность, должны иметь одинаковый периметр.

Но по изопериметрическому неравенству круг — это кривая, охватывающая максимальную площадь среди всех фигур с заданным периметром. Таким образом, окружность охватывает максимальную площадь среди всех фигур данного диаметра.

$\endgroup$

3
9н$. Это означает, что шар радиуса $\frac{1}{2}$ имеет наибольший объем среди всех фигур с диаметром не более $1$.