§ 13. Численность населения и размещение людей на Земле
Население Земли
§ 13. Численность населения и размещение людей на Земле
Вы узнаете:
•О численности населения Земли и её изменениях во времени.
•Что такое естественный прирост населения и от чего он зависит.
•Что такое миграции людей и каковы их причины.
•Как размещено население на Земле.
Вы научитесь:
•Анализировать графики изменения численности населения.
•Читать карту плотности населения.
•Выявлять причины неравномерности расселения людей.
•Находить информацию об адаптации людей к природным условиям.
Вспомните:
•Каковы внешние признаки людей различных рас? Как вы понимаете утверждение «Человек — часть биосферы»? Из уроков истории вспомните, где возникли первые земледельческие государства.
Обратитесь к электронному приложению
Численность населения Земли. В наши дни на Земле живёт более 7 млрд человек. Однако за 3—2 тыс. лет до н. э. на Земле проживало только 50 млн человек.
э. на Земле проживало только 50 млн человек.
|
Выполните задания практикума, помещённые после параграфа.
|
Численность населения определяют по переписям, которые теперь регулярно проводят во многих странах мира. Переписчики заполняют специальные переписные листы, по которым составляют характеристику населения по нескольким признакам (пол, возраст, образование, профессия и др.).
Рис. 42. Рост численности населения Земли
На основе переписей учёные составляют прогнозы численности населения мира. Предполагают, что к 2050 г. она составит более 8,5 млрд человек (рис. 42).
Причины, влияющие на численность населения. Изменения численности населения зависят от естественного прироста населения. Этот прирост определяется разницей между родившимися и умершими жителями. Рождаемость и смертность людей в странах мира различны. Во многих странах Африки рождается много детей, а умирает людей в три раза меньше. Поэтому естественный прирост населения в странах Африки довольно большой.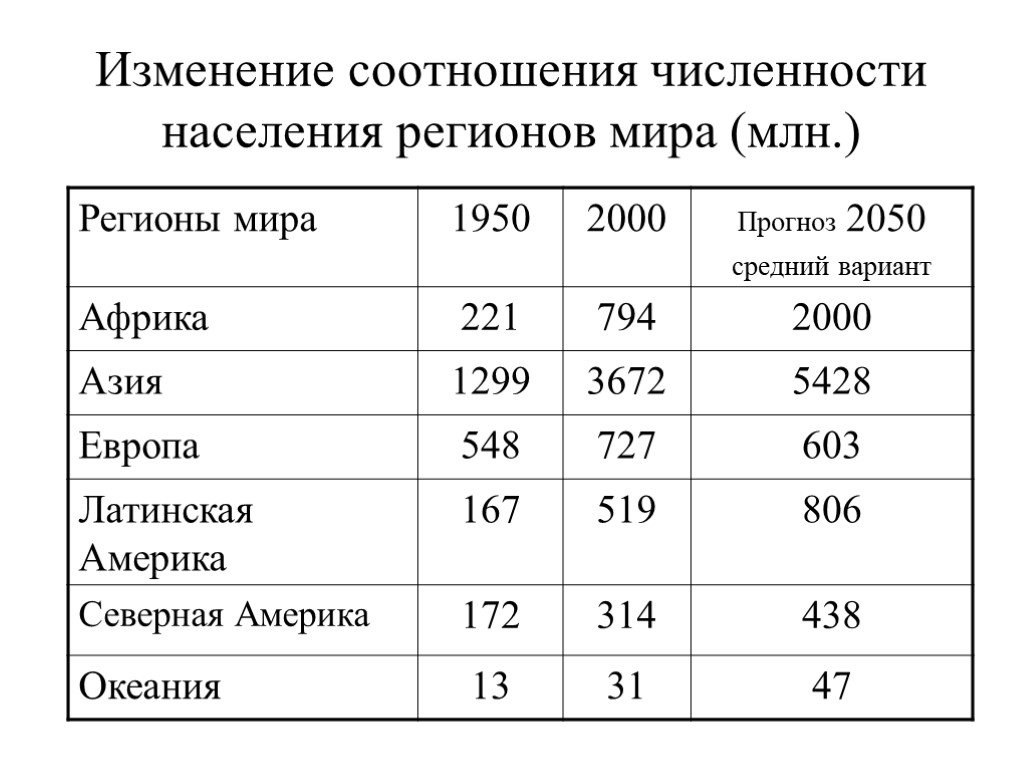 Во многих странах Европы, наоборот, число людей пожилого возраста велико, а детей рождается мало. В некоторых из этих стран наблюдается даже уменьшение численности населения, например в Италии, Болгарии.
Во многих странах Европы, наоборот, число людей пожилого возраста велико, а детей рождается мало. В некоторых из этих стран наблюдается даже уменьшение численности населения, например в Италии, Болгарии.
Прирост населения зависит от многих причин: от материальных условий жизни, культурных и религиозных традиций населения, условий труда, развития медицины и других факторов. (Приведите примеры.)
Величина естественного прироста оказывает влияние на возраст населения и продолжительность жизни. В странах с развитым хозяйством растёт доля старших возрастов, происходит старение населения (страны Европы, США, Канада). Например, в Японии продолжительность жизни 82 года. В бедных странах Африки этот возраст составляет всего 45—60 лет.
Рис. 43. Предполагаемые пути расселения человека
На численность населения немалое влияние оказывают миграции, т. е. переселение людей на новое место жительства. В различные исторические эпохи происходили значительные миграции людей (рис. 43).
|
Приведите примеры миграций, знакомые вам из уроков истории.
|
Арабы в VII—IX вв. заселили Северную Африку. Жители Западной и Южной Европы — Америку. Причины миграций различны: экономические (например, в поисках работы), политические, религиозные. Главные районы миграций в Европе — страны Западной Европы, куда едут рабочие из стран Средиземноморья. В США в поисках работы переселяются жители Мексики, стран Карибского моря.
|
Приведите свои примеры миграций людей и объясните их причины.
|
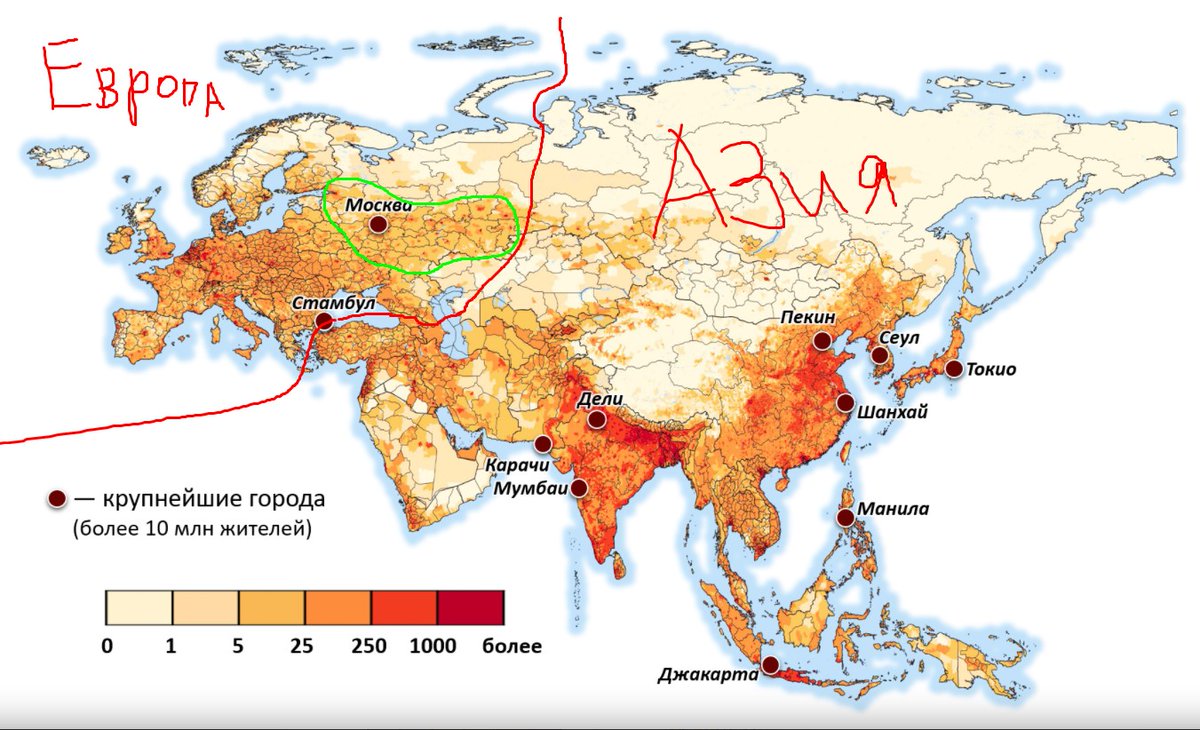
Размещение людей на Земле. Население размещается на Земле очень неравномерно.
Количество людей, приходящихся на 1 км2 площади, называют плотностью населения.
Плотность вычисляют путём деления численности населения на площадь. Средняя плотность населения Земли составляет немногим более 40 чел./км2. Однако этот показатель не даёт представления о контрастах размещения людей. Плотность существенно различается от места к месту.
Плотность существенно различается от места к месту.
|
Составьте по плану характеристику карты «Плотность населения». Определите наиболее и наименее заселённые территории материков.
|
Бо́льшая часть людей живёт на равнинах, вблизи морей и океанов, в умеренном, субтропическом и субэкваториальном климатических поясах.
Практикум
Численность населения Земли постоянно меняется. Однако эти изменения неодинаковы на разных материках и в разных странах. Происходящие изменения приводят ко многим сложным проблемам: чрезмерно быстрый рост численности населения вызывает трудности в снабжении продовольствием, чистой водой и другими природными богатствами. С некоторыми изменениями вы познакомитесь, выполнив задания 1—4.
1. Используя таблицу 1, сделайте вывод о темпах изменения численности населения земного шара.
Таблица 1
Рост численности населения земного шара
|
Годы
| ||||||
|
1650
|
1750
|
1850
|
1960
|
1999
|
2050 (прогноз)
| |
|
Численность населения, млрд чел.
|
0,55
|
0,725
|
1,2
|
3,0
|
6,0
|
8,7
|
2. Используя таблицу 2, определите: самый населённый регион; во сколько раз население Африки превышает население Южной Америки; во сколько раз население Европы превышает население Северной Америки.
Какой вывод можно сделать на основе анализа данных таблицы?
Таблица 2
Численность населения регионов Земли
|
Регионы
|
Численность населения, млн чел.
|
|
Азия
|
4300
|
|
Африка
|
1110
|
|
Европа (включая Россию)
|
745
|
|
Северная Америка
|
473
|
|
Южная Америка
|
480
|
|
Австралия и Океания
|
38
|
3.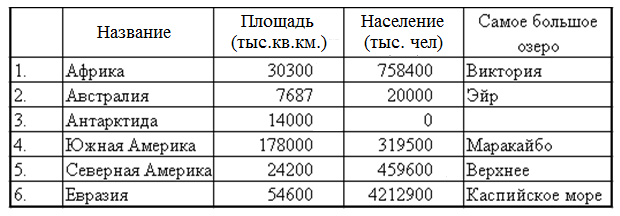 Используя карту атласа «Плотность населения», определите:
Используя карту атласа «Плотность населения», определите:
а) в каких регионах земного шара наибольшая плотность населения и чему она равна;
б) где на земном шаре плотность населения менее 1 чел./км2;
в) в какой части земного шара расположены незаселённые места;
г) какую закономерность подтверждают данные карты;
д) какие условия влияют на распределение населения по Земле.
4. Соберите информацию о рождаемости, смертности и приросте населения своей местности. Составьте графики и диаграммы по собранным данным.
Таблица материков планеты Земля: названия, площадь, население, особенности
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru ПОЛЕЗНО Материки планеты Земля: таблица
Ниже представлена таблица с шестью материками Земли, которая содержит их названия, площадь (в миллионах квадратных километров), процент от общей суши планеты, приблизительную численность населения и географические особенности, отличающие материк от всех остальных.
| Название материка | км<sup>2</sup></nobr>» data-order=»Площадь, <nobr>мнл. км<sup>2</sup></nobr>»>Площадь, мнл. км2 | Процент от общей суши Земли | Население (прибл.) | Географические особенности |
| Евразия | 53,760 | 36,2% | » data-order=»4,618 млрд.»>4,618 млрд. | 1. Самый крупный материк с наибольшей численностью населения. 2. Единственный материк, омываемый 4 океанами. |
| Африка | 30,370 | 20,4% | » data-order=»1,216 млрд.»>1,216 млрд. | 1. Самый жаркий материк. 2. Считается прародиной человечества. |
| Северная Америка | 24,710 | 16,6% | 579 млн. | Нет стран без выхода к морю.<br> 2. К материку относится самый крупный остров — Гренландия.» data-order=»1. Нет стран без выхода к морю.<br> 2. К материку относится самый крупный остров — Гренландия.»>1. Нет стран без выхода к морю. 2. К материку относится самый крупный остров — Гренландия. |
| Южная Америка | 17,840 | 12% | 425 млн. | » data-order=»Самый влажный и «зеленый» материк.»>Самый влажный и «зеленый» материк. |
| Австралия | 7,692 | 5,2% | 23 млн. | «>1. Самый маленький и засушливый материк. 2. Включает только одно одноименное государство — Австралия. |
| Антарктида | 14,200 | 9,6% | 1-5 тыс. (сотрудники полярных станций) | «>На материке нет ни одного государства, а также постоянно проживающего населения. |
Примечания:
Материк – большой массив суши, омываемый со всех сторон океанами и морями. Иногда материки называют континентами, что в целом допустимо, однако между этими понятиями есть разница.
Континент – это крупный массив земной коры, большая часть которого не покрыта океаном, а крайние участки расположены ниже уровня океана.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Идентичность по происхождению среди населения острова и материка
Сравнительное исследование
. 1995 г., январь; 139(1):429-37.
1995 г., январь; 139(1):429-37.
doi: 10.1093/генетика/139.1.429.
Б Раннала
1
, J A Hartigan
принадлежность
- 1 Факультет биологии, Йельский университет, Нью-Хейвен, Коннектикут 06520.
PMID:
7598763
PMCID:
PMC1206339
DOI:
10.1093/генетика/139.1.429
Бесплатная статья ЧВК
Сравнительное исследование
B Rannala et al.
Генетика.
1995 января
Бесплатная статья ЧВК
. 1995 г., январь; 139(1):429-37.
doi: 10.1093/генетика/139.1.429.
Авторы
Б Раннала
1
, Дж. А. Хартиган
принадлежность
- 1 Факультет биологии, Йельский университет, Нью-Хейвен, Коннектикут 06520.
PMID:
7598763
PMCID:
PMC1206339
DOI:
10.1093/генетика/139.1.429
Абстрактный
Представлена новая модель генетической структуры среди группы островных популяций с колеблющимися размерами популяций и непрерывным перекрытием поколений с использованием стохастического процесса рождения, смерти и иммиграции (BDI).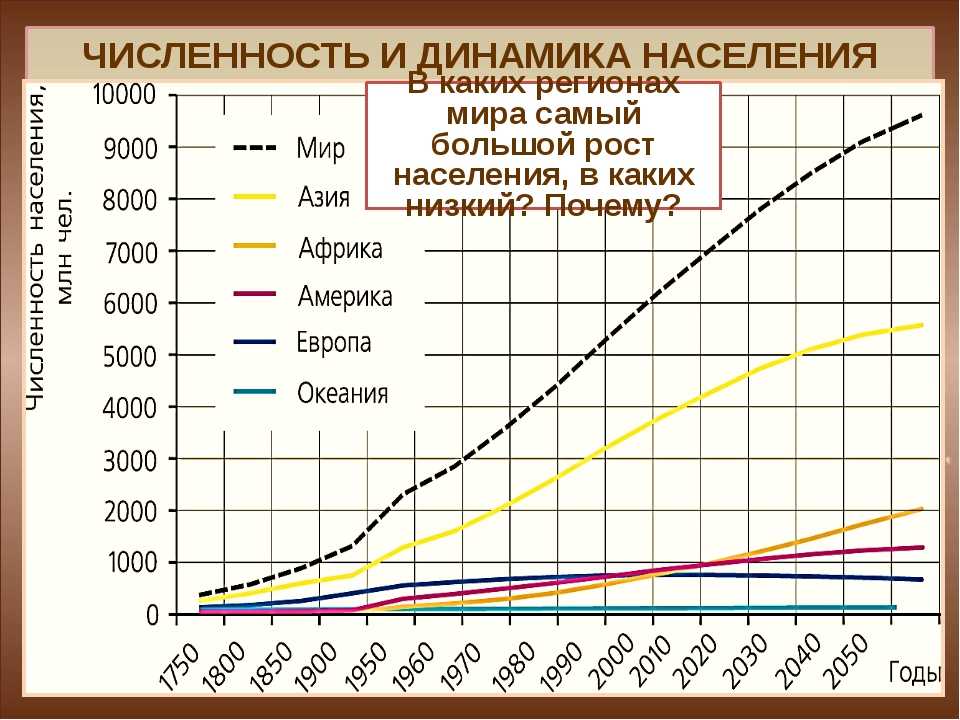 Иммигранты прибывают на каждый остров из большого населения материка с постоянной частотой генов в соответствии с процессом Пуассона. Средняя вероятность идентичности по происхождению (ВЗК) для двух гаплоидных особей, случайно выбранных из островной популяции, равна f0 = (phi f1 + лямбда)/(фи + лямбда), где f1 — вероятность ВЗК для двух случайно выбранных иммигрантов, лямбда — уровень рождаемости для каждого человека, а phi — уровень прибытия иммигрантов на каждый остров. Значение f0 не зависит от процесса гибели, времени и N. Ожидаемый уровень генетической дифференциации островных популяций FST = (1 — 1/n)lambda/(phi + lambda), где n — общее количество островков. прием иммигрантов. Поскольку f0 и FST не зависят от процесса смерти, для модели BDI генетическая структура популяции для нескольких общих демографических ситуаций может быть исследована с использованием наших уравнений. К ним относятся стохастический экспоненциальный или логистический (регулируемый уровнем смертности) рост внутри островов или структура населения «источник-приемник».
Иммигранты прибывают на каждый остров из большого населения материка с постоянной частотой генов в соответствии с процессом Пуассона. Средняя вероятность идентичности по происхождению (ВЗК) для двух гаплоидных особей, случайно выбранных из островной популяции, равна f0 = (phi f1 + лямбда)/(фи + лямбда), где f1 — вероятность ВЗК для двух случайно выбранных иммигрантов, лямбда — уровень рождаемости для каждого человека, а phi — уровень прибытия иммигрантов на каждый остров. Значение f0 не зависит от процесса гибели, времени и N. Ожидаемый уровень генетической дифференциации островных популяций FST = (1 — 1/n)lambda/(phi + lambda), где n — общее количество островков. прием иммигрантов. Поскольку f0 и FST не зависят от процесса смерти, для модели BDI генетическая структура популяции для нескольких общих демографических ситуаций может быть исследована с использованием наших уравнений. К ним относятся стохастический экспоненциальный или логистический (регулируемый уровнем смертности) рост внутри островов или структура населения «источник-приемник». Поскольку ожидаемые значения как f0, так и FST не зависят от времени, они достигаются немедленно для BDI. модели, без необходимости предполагать, что островные популяции находятся в генетическом равновесии.
Поскольку ожидаемые значения как f0, так и FST не зависят от времени, они достигаются немедленно для BDI. модели, без необходимости предполагать, что островные популяции находятся в генетическом равновесии.
Похожие статьи
Теория выборки нейтральных аллелей в островном населении колеблющегося размера.
Раннала Б.
Раннала Б.
Теория народной биологии. 1996 авг; 50 (1): 91-104. doi: 10.1006/tpbi.1996.0024.
Теория народной биологии. 1996.PMID: 8813016
Оценка потока генов в островных популяциях.
Раннала Б., Хартиган Дж.А.
Раннала Б. и др.
Генет Рез. 1996 г., апрель; 67 (2): 147–58. дои: 10.1017/s0016672300033607.
Генет Рез. 1996.PMID: 8801187
Генетическая структура популяции комаров Anopheles gambiae на островах озера Виктория, западная Кения.

Чен Х., Минакава Н., Бейер Дж., Ян Г.
Чен Х и др.
Малар Дж. 2004 г., 6 декабря; 3:48. дои: 10.1186/1475-2875-3-48.
Малар Дж. 2004.PMID: 15581429Бесплатная статья ЧВК.
Генетические и филогенетические следствия островной биогеографии.
Джонсон К.П., Адлер Ф.Р., Черри Д.Л.
Джонсон КП и др.
Эволюция. 2000 г., апрель; 54(2):387-96. doi: 10.1111/j.0014-3820.2000.tb00041.x.
Эволюция. 2000.PMID: 10937215
Анализ микросателлитной изменчивости у Pinus radiata выявляет эффекты генетического дрейфа, но не недавние узкие места.
Карху А., Фогль С., Моран Г.Ф., Белл Дж.С., Саволайнен О.
Карху А. и др.
Дж. Эвол Биол. 2006 Январь; 19 (1): 167-75. doi: 10.1111/j.1420-9101.2005.00982. x.
x.
Дж. Эвол Биол. 2006.PMID: 16405588
Посмотреть все похожие статьи
Цитируется
Теория островной биогеографии объясняет генетическое разнообразие фрагментированной каменной куропатки (9).0113 Lagopus muta ) популяция.
Костанци Дж. М., Штайфеттен Ø.
Костанци Дж. М. и соавт.
Эколь Эвол. 2019 27 февраля; 9 (7): 3837-3849. doi: 10.1002/ece3.5007. Электронная коллекция 2019 апр.
Эколь Эвол. 2019.PMID: 31015970
Бесплатная статья ЧВК.Вывод на основе правдоподобия в моделях изоляции по расстоянию с использованием пространственного распределения низкочастотных аллелей.
Новембр Ж, Слаткин М.
Новембре Дж. и соавт.
Эволюция. 2009 ноябрь;63(11):2914-25. doi: 10. 1111/j.1558-5646.2009.00775.x. Epub 2009 16 июля.
1111/j.1558-5646.2009.00775.x. Epub 2009 16 июля.
Эволюция. 2009.PMID: 19624728
Бесплатная статья ЧВК.Метод интегрированного правдоподобия для оценки генетической дифференциации между популяциями.
Китакадо Т., Китада С., Кишино Х., Скауг Х.Дж.
Китакадо Т. и др.
Генетика. 2006 г., август; 173 (4): 2073-82. doi: 10.1534/genetics.106.055350. Epub 2006 4 июня.
Генетика. 2006.PMID: 16751669Бесплатная статья ЧВК.
Вероятность идентичности по происхождению в метапопуляциях.
Кай И., Ласко М.
Кай И и др.
Генетика. 1999 июль; 152 (3): 1217-28. doi: 10.1093/генетика/152.3.1217.
Генетика. 1999.PMID: 10388835
Бесплатная статья ЧВК.Динамика популяции, полученная по временным вариациям микросателлитных локусов у самоопыляющейся улитки Bulinus truncatus.

Виар Ф., Джасти Ф., Ярн П.
Виард Ф. и соавт.
Генетика. 1997 г., июль; 146 (3): 973–82. doi: 10.1093/генетика/146.3.973.
Генетика. 1997.PMID: 9215901
Бесплатная статья ЧВК.
Рекомендации
Генетика. 1964 Апрель; 49: 725-38
—
пабмед
Теория народной биологии. 1977 декабрь; 12 (3): 253-62
—
пабмед
Генетика.
 1964 Апрель; 49 (4): 561-76
1964 Апрель; 49 (4): 561-76—
пабмед
Генетика. 1984 г., февраль; 106 (2): 293–308.
—
пабмед
Proc Natl Acad Sci U S A. 1980 Nov; 77(11):6710-4
—
пабмед
Типы публикаций
термины MeSH
Прикладная популяционная генетика
Подразделение происходит, когда особи пространственно, экологически или временно разделены, в результате чего относительная вероятность спаривания среди особей неравномерно распределяется среди всех особей. Это естественное состояние для большинства видов — они не спариваются совершенно случайно — и поэтому это вызывает изменения в том, как распределяется генетическая изменчивость. В этой главе мы исследуем подразделение и то, как мы количественно определяем его силу.
Это естественное состояние для большинства видов — они не спариваются совершенно случайно — и поэтому это вызывает изменения в том, как распределяется генетическая изменчивость. В этой главе мы исследуем подразделение и то, как мы количественно определяем его силу.
Прежде чем мы углубимся в обсуждение моделей, описывающих подразделение населения, нам, вероятно, следует прояснить некоторые термины, которые обычно используются при описании этих систем.
Миграция: Миграция – это перемещение людей между пространственными местоположениями. Строго говоря, это не означает никакого отношения к спариванию. Птицы, млекопитающие и даже насекомые мигрируют в зависимости от годовой сезонности, хотя процесс перемещения к экватору или более подходящей среде обитания для конкретного сезона не обязательно влияет на генетическую структуру популяции.
Поток генов: Поток генов — это процесс перемещения генетического материала между регионами или популяциями, что приводит к модификации существующих генетических вариаций. Поток генов обычно обозначается как скорость (например, доля между 0 и 1) и оказывает прямое влияние на аллельный и/или генотипический состав популяции.
Поток генов обычно обозначается как скорость (например, доля между 0 и 1) и оказывает прямое влияние на аллельный и/или генотипический состав популяции.
Это не означает, что миграция может привести к последующему спариванию, внося свой вклад в структуру популяции, просто это не обязательно требуется.
17.1 Модели разделения
Если индивиды разделены на разные группы, ожидаемые частоты аллелей и генотипов зависят от того, каким образом популяции связаны потоком генов. Есть несколько классических моделей, связанных со связностью населения, которые мы рассмотрим в этом разделе, хотя в действительности способы, которыми на самом деле связаны популяции, скорее всего, выходят за рамки строгих соглашений для этих простых моделей. Однако эти модели предоставляют нам основу для изучения наблюдаемого распределения генетической изменчивости и для предсказания будущей структуры с учетом нескольких предположений.
Для описания связности здесь будет использоваться сетевая аналогия, при этом популяции действуют как узлы в сети, а поток генов обозначается ребрами, соединяющими эти узлы. Строго говоря, это взвешенный граф, поскольку с ребрами связаны определенные числовые значения, представляющие скорость миграции между связанными ребрами. Каждая популяция может иметь свои собственные частотные спектры аллелей, и со временем частоты аллелей могут меняться в ответ на иммиграцию в популяцию, но не ожидается, что они изменятся из-за эмиграции из нее, поскольку мы предполагаем, что вероятность миграции любого человека статистически не зависит от аллеля. частоты.
Строго говоря, это взвешенный граф, поскольку с ребрами связаны определенные числовые значения, представляющие скорость миграции между связанными ребрами. Каждая популяция может иметь свои собственные частотные спектры аллелей, и со временем частоты аллелей могут меняться в ответ на иммиграцию в популяцию, но не ожидается, что они изменятся из-за эмиграции из нее, поскольку мы предполагаем, что вероятность миграции любого человека статистически не зависит от аллеля. частоты.
17.2 Модель материка острова
Модель остров-материк — это простейшая формулировка модели населения. Здесь у нас есть большое население материка и небольшое население островов. Для простоты определите частоты аллелей этих двух как \(p_x\) и \(p_y\). В каждом дискретном поколении некоторая часть \(m\) особей с материка попадает в брачную популяцию особей на острове. Состав острова состоит из доли \(m\) лиц, являющихся иммигрантами, и доли \((1-m)\), которые уже находились на острове.
Рисунок 17. 1: Базовая модель распределения населения между материком и островом.
1: Базовая модель распределения населения между материком и островом.
В следующем поколении частоты аллелей материкового населения остаются прежними (мы предполагаем, что они достаточно велики, чтобы потеря мигрантов не влияла на аллельные или генотипические частоты), тогда как островное население состоит из \(m \) процент иммигрантов, частота которых равна \(p_x\), и \((1-m)\) доля жителей, частота которых была в последнем поколении \(p_y\). В совокупности их частоты составляют:
\[
p_{y,t+1} = (1-m)p_{y,t} + mp_{x,t}
\]
Из этой формулировки легко сделать вывод, что через достаточное количество поколений частоты аллелей материка и острова будут одинаковыми. Остров в конечном итоге будет иметь те же частоты, что и материк, хотя количество времени, которое требуется для этого, зависит от разницы в частотах аллелей, \(\delta p = p_x — p_y\), и скорости миграции, \(m\), к населению острова. Поскольку миграция с острова на материк отсутствует, равновесная частота будет равна \(p_x\). Вот небольшой код, показывающий влияние различных скоростей миграции.
Вот небольшой код, показывающий влияние различных скоростей миграции.
migration_rates <- c(.01,.05,.10,.15)
результаты <- data.frame (m = rep (migration_rates, каждый = 100),
Поколение = повтор (1: 100, раз = 4),
р=нет данных)
for( m в migration_rates) {
пкс <- 0
ру <- 1
результаты$p[ результаты$m==m ] <- py
for(t в 2:100){
p.0 <- результаты$p[результаты$m==m & results$Generation == (t-1)]
т.1 <- (1-м)*т.0 + рх*м
результаты$p[ результаты$m==m & results$Generation == t] <- p.1
}
}
результаты $m <- фактор(результаты $m) Рисунок 17.2: Частоты аллелей для и население острова, зафиксированные для аллеля а, который получает мигрантов из материкового населения с разной скоростью (\(m\)), у которого аллель отсутствует на острове.
Таким образом, даже при низкой миграции, скажем \(m=0,01\), частоты аллелей могут меняться довольно быстро из-за иммиграции.
17.3 Модель острова
Следующей по сложности моделью является модель, в которой каждое население обменивается мигрантами.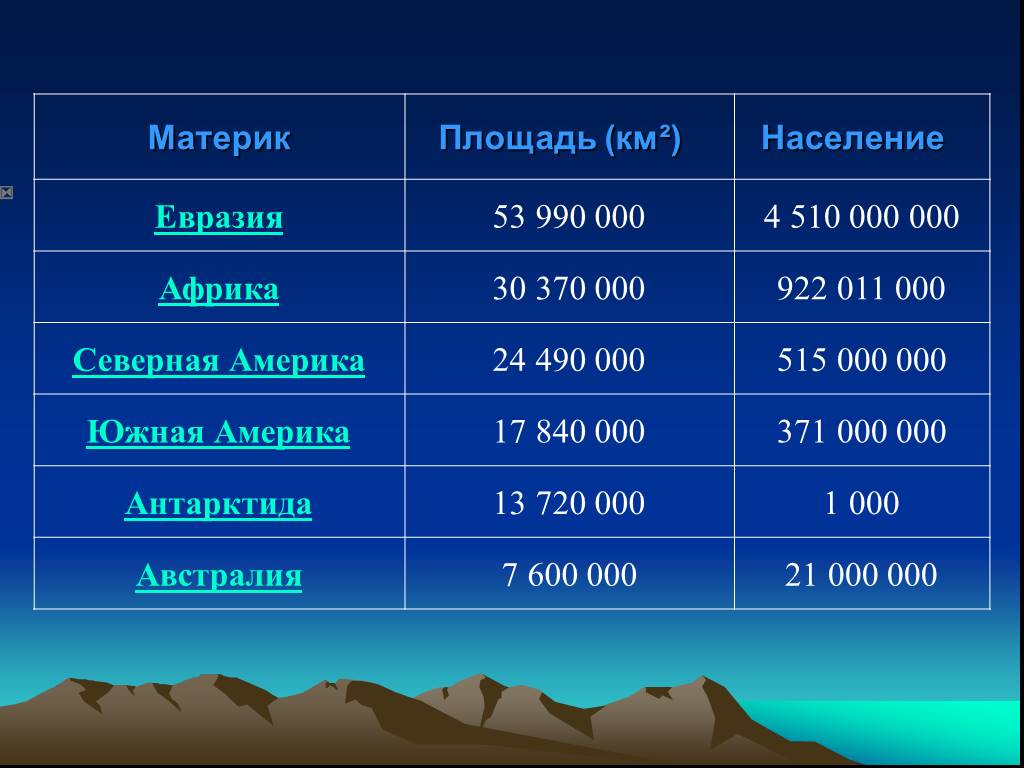 Эта модель n-островов была впервые представлена Сьюэллом Райтом (19 лет).31). В этом случае все популяции связаны постоянной скоростью миграции. Аллель, возникший в одной популяции в результате мутации, потенциально может распространиться на любую другую популяцию в одном поколении, вероятность которого определяется скоростью миграции.
Эта модель n-островов была впервые представлена Сьюэллом Райтом (19 лет).31). В этом случае все популяции связаны постоянной скоростью миграции. Аллель, возникший в одной популяции в результате мутации, потенциально может распространиться на любую другую популяцию в одном поколении, вероятность которого определяется скоростью миграции.
Рисунок 17.3: Модель n-островов с тремя популяциями, каждая со своими частотами аллелей, с постоянной и симметричной скоростью миграции (\(m\)).
Стабильность этой системы достаточно высока. Все популяции имеют общих мигрантов, и, как следствие, все популяции, таким образом, будут сходиться к единой частоте аллеля, определяемой глобальной средней частотой аллеля, \(\bar{p}\). Время, необходимое для достижения этой точки равновесия, определяется тем, насколько далеко от глобального среднего находится население, и скоростью, с которой распределяются мигранты.
Существует два способа моделирования такой системы, один проще другого. Самый простой способ — считать, что мигранты — это гигантский пул мигрантов, и от этого они распределяются по популяциям. Например, если \(\bar{p}\) является глобальной средней частотой аллеля, можно считать, что пул мигрантов также имеет эту частоту аллеля. Если вы считаете, что это разумное приближение, то частоты аллелей в следующем поколении, скажем, для популяции \(X\) на рис. 17.3, будут: 9т
Самый простой способ — считать, что мигранты — это гигантский пул мигрантов, и от этого они распределяются по популяциям. Например, если \(\bar{p}\) является глобальной средней частотой аллеля, можно считать, что пул мигрантов также имеет эту частоту аллеля. Если вы считаете, что это разумное приближение, то частоты аллелей в следующем поколении, скажем, для популяции \(X\) на рис. 17.3, будут: 9т
df <- data.frame( Генерация = 1:T, Частота = pX)
Рисунок 17.4: Изменение частоты аллелей для популяции, начинающейся с \(p_X=0,1\) и принимающей мигрантов из глобального пула мигрантов \(p_m=0,5\) со скоростью \(m=0,05\).
Со временем частоты аллелей систематически изменяются, стремясь к глобальной частоте аллелей, определенной для всех популяций.
Некоторые существенные предположения для этой модели включают:
- Поколения не перекрываются, так что мы можем использовать подход разностного уравнения для понимания связности.
- Популяции дискретны в том смысле, что между популяциями есть разрывы.

- Скорость миграции постоянна как в пространстве, так и во времени.
- Миграция симметрична в обоих направлениях.
Этот подход может быть не самым реалистичным, но он описывает общий способ, с помощью которого мы можем предсказывать частоты аллелей во времени.
17.4 Ступенчатые модели
Несколько более реалистичная модель была предложена Kimura & Weiss (1964), которые ввели термин «ступенчатая» модель для обозначения модели, учитывающей пространственное расположение популяций при описании связности.
Рисунок 17.5: Одномерная модель ступени. Каждая популяция связана только с двумя другими и обменивается мигрантами со скоростью \(\frac{m}{2}\) в каждом направлении в каждом поколении.
Их модель состояла из бесконечного числа популяций, связанных с единой скоростью миграции \(m\). Для любой популяции в этом континууме частота аллелей в следующем поколении зависела от следующего:
- Частота в текущем поколении для этой популяции \(p_i\).

- Скорость, с которой мигранты прибывали к населению с каждой стороны. Предполагалось, что общий уровень миграции был \(m\), и поэтому они принимали мигрантов со скоростью \(\frac{m}{2}\) в каждом поколении от каждого соседа.
- У каждого соседа может быть собственная начальная частота аллеля, которая со временем будет меняться при продолжающемся обмене мигрантами.
- Существует некоторый «фоновый» уровень миграции, состоящий из некоторой доли мигрантов, \(m_{\infty}\), чьи частоты аллелей обозначаются как \(p_{\infty}\). Эту часть уравнения может быть немного сложно параметризовать (или, говоря другими словами, это может быть хорошим «буфером» в вашей модели, помогающим объяснить вещи, которые вы не можете объяснить напрямую). 92] = \frac{p_i(1-p_i)}{2N_e}\), что согласуется с тем, что мы уже видели для дрейфа.
В целом их формулировка такова:
\[
p_{i,t+1} = (1-m_1-m_\infty)*p_i + \frac{m}{2}(p_{i-1,t} + p_{i+1,t}) + m_ \infty\bar{p} + \eta_i
\]
Расширяя эту базовую модель, они также получили ожидания для двумерной модели связности, в которой популяции были выстроены в сетку со строками и столбцами. Они также ненадолго развлеклись трехмерной моделью.
Они также ненадолго развлеклись трехмерной моделью.
Для каждой из этих моделей оценено математическое ожидание уменьшения генетической корреляции между парами популяций при увеличении расстояния между популяциями. Возможно, неудивительно, что корреляция выше в одномерных, чем в двухмерных схемах. Он также выше в 2-мерных, чем в 3-мерных. Их статья представляет собой отличное введение в математику, лежащую в основе связности в дискретном пространстве, и ее следует подробно изучить тем, кто заинтересован в более полном моделировании этого явления. Однако для полноты здесь мы рассмотрим более общий подход к пониманию связности и изменений в частотах аллелей, основанный на определенной «сети» связности.
17.5 Общая модель
Более широкий подход, который можно применять ко всем типам моделей связности, заключается в том, что он позволяет определить базовую модель связности, а затем оценить изменения частоты аллелей в этой модели. Вместо того, чтобы иметь единую скорость миграции для всех популяций или жесткое расположение популяций, если вы можете указать топологию сети связи, вы можете использовать следующий подход для оценки изменений частоты аллелей.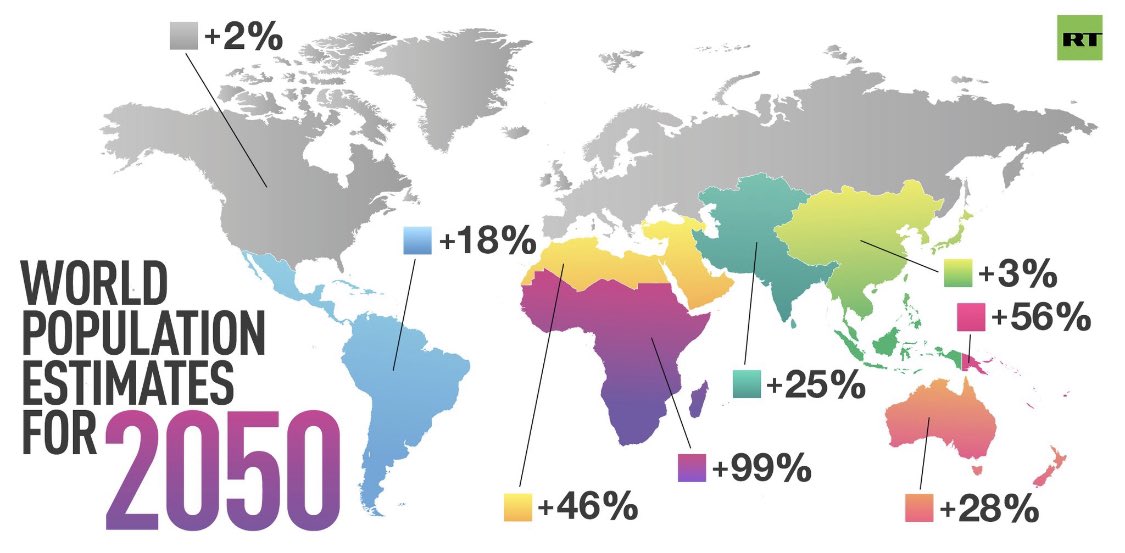 Мы начнем с простого случая трех популяций, каждая со своими частотами и связанными индивидуальными темпами миграции. В этой системе мы можем рассматривать частоты для популяции X как производные от частот всех популяций, с которыми она обменивается мигрантами, а также их индивидуальных показателей. Вот пример из диаграммы ниже.
Мы начнем с простого случая трех популяций, каждая со своими частотами и связанными индивидуальными темпами миграции. В этой системе мы можем рассматривать частоты для популяции X как производные от частот всех популяций, с которыми она обменивается мигрантами, а также их индивидуальных показателей. Вот пример из диаграммы ниже.
\[
p_{x,t+1} = m_{x \leftrightarrow y}p_{y,t} + m_{x \leftrightarrow z}p_{z,t} + [1 - (m_{x \leftrightarrow y} + m_ {x \leftrightarrow z})]p_x
\]
Рисунок 17.6: Общая мультипопуляционная модель потока генов с индивидуальными скоростями миграции.
Текущая частота определяется частотами всех связанных популяций (как \(Y\), так и \(Z\) в данном случае) в предыдущем поколении и их индивидуальными коэффициентами миграции (это иммигранты) и жителей ( \(1 - m_{все\;миграции\;в\;данную\;популяцию}\)) и его предыдущую частоту аллеля. Аналогичным образом, другие популяции:
\[
p_{y,t+1} = m_{x \leftrightarrow y}p_{x,t} + m_{y \leftrightarrow z}p_{z,t} + [1 - (m_{x \leftrightarrow y} + m_ {y \leftrightarrow z})]p_y
\]
и
\[
p_{z,t+1} = m_{x \leftrightarrow z}p_{x,t} + m_{y \leftrightarrow z}p_{y,t} + [1 - (m_{x \leftrightarrow z} + m_ {y \leftrightarrow z})]p_z
\]
В R мы можем перебрать это и увидеть эти поведения. Здесь мы рассматриваем три популяции, каждая из которых начинается с разных частот аллелей, и оцениваем частоты аллелей за период T = 75 поколений.
Здесь мы рассматриваем три популяции, каждая из которых начинается с разных частот аллелей, и оцениваем частоты аллелей за период T = 75 поколений.
Т <- 75 pX <- rep(NA,T) pY <- rep(NA,T) pZ <- rep(NA,T) рХ[1] <- 0,1 pY[1] <- 0,5 pZ[1] <- 0,9
Эти популяции обмениваются мигрантами с разным базовым уровнем. В этом примере мы предположим, что обмен мигрантами симметричен, хотя это и не обязательно, и вы можете видеть, как следующий код расширяется для учета асимметрии.
mXY <- 0,04 мXZ <- 0,02 mYZ <- 0,08
Затем моделирование выполняется для T поколений, и на каждой итерации частоты каждой популяции обновляются на основе этих показателей миграции и частот популяций, из которых происходят иммигранты.
для (генерал в 2:T){
pX[gen] <- mXY*pY[gen-1] + mXZ*pZ[gen-1] + ( 1 - (mXY+mXZ))*pX[gen-1]
pY[gen] <- mXY*pX[gen-1] + mYZ*pZ[gen-1] + ( 1 - (mXY+mYZ))*pY[gen-1]
pZ[gen] <- mXZ*pX[gen-1] + mYZ*pY[gen-1] + ( 1 - (mYZ+mXZ))*pZ[gen-1]
}
df <- data. frame( Generation=rep(1:T,times=3))
df$Frequency=c(pX,pY,pZ)
df$Population <- rep(c("X","Y","Z"), each=T)
frame( Generation=rep(1:T,times=3))
df$Frequency=c(pX,pY,pZ)
df$Population <- rep(c("X","Y","Z"), each=T) С течением времени мы видим, что все частоты аллелей сходятся на глобальной частоте аллелей
mean( c( рХ,рУ,рZ))
## [1] 0,5
Рисунок 17.7: Изменение частот аллелей во времени для трех популяций, связанных разной скоростью потока генов (\(m_{XY} = 0,04\), \(m_{XZ}=0,02\), \(m_{YZ}=0,08 \)).
Здесь нужно сделать пару замечаний.
- Скорость изменения частот аллелей зависит от \(\delta p = p_i - \bar{p}\) и скорости миграции. Подход к \(\bar{p}\) был быстрее для населения \(Z\), чем для населения \(X\), поскольку скорость миграции в \(X\) и из него в целом ниже, чем из \(Z\) .
- Некоторые ситуации, в зависимости от конфигурации «сети» связности, могут привести к реверсированию направления изменения частоты аллелей. Посмотрите на население \(Y\). Его частоты аллелей начинались с \(\bar{p}\) и первоначально увеличивались до частот популяции \(Z\).
 Это связано с тем, что относительная скорость миграции между \(Y\) и \(Z\) больше, чем между \(Y\) и \(X\).
Это связано с тем, что относительная скорость миграции между \(Y\) и \(Z\) больше, чем между \(Y\) и \(X\).
Эти наблюдения показывают, что при моделировании необходимо немного подождать, чтобы динамика системы немного «прогорела». Точка равновесия, которую мы хотим увидеть, достижима только после того, как вся система прошла через множество поколений и все особенности были тщательно повторены.
17.6 Общие стратегии
Имея дело с подобными динамическими системами, необходимо учитывать некоторые важные моменты, пытаясь понять лежащую в их основе динамику. Это общие правила, хотя всегда есть исключения. Однако, если вы будете следовать им, вам, вероятно, будет намного легче с вычислениями.
- Протяни сеть, если сможешь. Если это слишком сложно, то хотя бы попробуйте зафиксировать основные потоки по сети графически. Визуализация сетевой структуры очень полезна для понимания того, куда, по вашему мнению, должны двигаться дела.
- В большинстве систем частоты аллелей будут стремиться к \(\bar{p}\) для всех популяций при достаточном количестве времени.


Leave a Reply